오예 !!!
[ML] HA2 part1 (1) Decision trees with Breast cancer dataset 본문
📢 학교 수업에서 수행한 과제입니다.
HA2 part1은 'Decision trees with Breast cancer dataset'과 'RandomForest with Titanic dataset' 두 가지로 이루어져 있다.
이번 게시글에서는 우선 Decision trees에 대해 다룰 것이다.
구글 코랩에서 코드를 작성 및 실행하였으며, 전체 코드는 다음 코랩 노트북을 참고하라.
https://colab.research.google.com/drive/1luQJnz2s9UGT7iZi5NFg7XwBo5RyDysq?usp=sharing
HA2_part1.ipynb
Colaboratory notebook
colab.research.google.com
그럼 우선 Breast cancer dataset을 불러온다.
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
data = datasets.load_breast_cancer()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1
)Node & Decision Tree classes를 정의해준다. 이때, gini importance를 사용해주었다.
class Node:
def __init__(self, feature=None, value=None, left=None, right=None, *, label=None):
self.feature = feature
self.value = value
self.left = left
self.right = right
self.label = label
def is_leaf(self):
return self.label is not None
class DecisionTree:
def __init__(self, max_depth=100, min_samples_split=2):
self.max_depth = max_depth
self.min_samples_split = min_samples_split
self.root = None
def _stop(self, depth):
if (depth >= self.max_depth
or self.n_class_labels == 1
or self.n_samples < self.min_samples_split):
return True
return False
def _gini_importance(self, y):
weights = np.bincount(y) / len(y)
gini_importance = 1 - np.sum([w ** 2 for w in weights if w > 0])
return gini_importance
def _expand_tree(self, X, value):
# np.argwhere: return indices of X which are less than and equal to value
# np.flatten: turn multi-dimensional data into vectors
left_idx = np.argwhere(X <= value).flatten()
# return indices of X which are greater than
right_idx = np.argwhere(X > value).flatten()
return left_idx, right_idx
def _impurity_decrease(self, X, y, value):
parent_gini_importance = self._gini_importance(y)
# expend the tree with X
left_idx, right_idx = self._expand_tree(X, value)
n, n_left, n_right = len(y), len(left_idx), len(right_idx)
if n_left == 0 or n_right == 0:
return 0
children_gini_importance = (n_left / n) * self._gini_importance(y[left_idx]) + (n_right / n) * self._gini_importance(y[right_idx])
return parent_gini_importance - children_gini_importance
def _best_split(self, X, y, features):
# create split dict in which we record score, feature, and value to keep the split yielding the maximum score
split = {'score':- 1, 'feat': None, 'value': None}
# for each column in 30 columns
for feat in features:
# select one feature column
# example: values in outlook column
X_feat = X[:, feat]
# np.unique: remove duplicates
# create values
values = np.unique(X_feat)
# for each value in the column
for value in values:
# compute the impurity decrease
score = self._impurity_decrease(X_feat, y, value)
# Update the split with the maximum score
if score > split['score']:
split['score'] = score
split['feat'] = feat
split['value'] = value
# return the best split with the maximum score (i.e., impurity decrease)
return split['feat'], split['value']
def _build_tree(self, X, y, depth=0):
self.n_samples, self.n_features = X.shape
self.n_class_labels = len(np.unique(y))
# 1. Check whether go or stop: use stopping criteria using _stop function
if self._stop(depth):
most_common_Label = np.argmax(np.bincount(y))
return Node(label=most_common_Label)
# 2. find the best split: get the best feature for the current node among 30 features
# random_f carries shuffled feature indices
random_f = np.random.choice(self.n_features, self.n_features, replace=False)
best_feat, best_value = self._best_split(X, y, random_f)
# 3. expand the tree: create the subtrees using the best split
left_idx, right_idx = self._expand_tree(X[:, best_feat], best_value)
# 4. grow the left subtree and right subtree recursively
left_child = self._build_tree(X[left_idx, :], y[left_idx], depth + 1)
right_child = self._build_tree(X[right_idx, :], y[right_idx], depth + 1)
return Node(best_feat, best_value, left_child, right_child)
def fit(self, X, y):
self.root = self._build_tree(X, y)
# For the evaluation using the testing set, we need a traverse function
def _traverse_tree(self, x, node):
if node.is_leaf():
return node.label
# recursively traverse the tree (left subtree)
# node.feature = feature index, so compare X to current node's value
if x[node.feature] <= node.value:
return self._traverse_tree(x, node.left)
# recursively traverse the tree (right subtree)
return self._traverse_tree(x, node.right)
def predict(self, X):
predictions = [self._traverse_tree(x, self.root) for x in X]
return np.array(predictions)이제 train set을 이용하여 Decision tree model을 학습한다.
clf = DecisionTree(max_depth = 10)
clf.fit(X_train, y_train)accuracy 함수를 다음과 같이 정의해주었다.
def accuracy(y_true, y_pred):
accuracy = np.sum(y_true == y_pred) / len(y_true)
return accuracy학습한 모델의 accuracy를 출력해보자.
y_pred = clf.predict(X_test)
acc = accuracy(y_test, y_pred)
print("Accuracy: ", acc)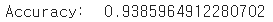
94% 정도의 accuracy가 나온 것을 확인할 수 있다.
'💻 > 기계학습' 카테고리의 다른 글
| [ML] HA2 part2 PCA & K-NN (0) | 2023.02.08 |
|---|---|
| [ML] HA2 part1 (2) RandomForest with Titanic dataset (1) | 2022.12.19 |
| [ML] HA1 part2 Support vector machines with Iris dataset (0) | 2022.12.19 |
| [ML] HA1 part1 (3) Gaussian discriminant analysis (Gaussian Naive Bayes) with iris dataset (0) | 2022.12.19 |
| [ML] HA1 part1 (2) Logistic regression with Titanic dataset (0) | 2022.12.19 |
Comments



